A graph is a kind of data structure, which is a collection of nodes, called vertices and line segments called arcs or edges that connect pairs of nodes.
In the concept of mathematics, a graph G is defined as follows: G=(V,E), where V is a finite, non-empty set of vertices (singular vertex) and E is a set of edges (links between pairs of vertices). When the edges in a graph have no direction, the graph is called undirected, otherwise called directed.
Cycle:A cycle is a path consisting of at least three vertices that starts and ends with same vertex. Two vertices are said to be connected if there is a path between them.
In the concept of mathematics, a graph G is defined as follows: G=(V,E), where V is a finite, non-empty set of vertices (singular vertex) and E is a set of edges (links between pairs of vertices). When the edges in a graph have no direction, the graph is called undirected, otherwise called directed.
Cycle:A cycle is a path consisting of at least three vertices that starts and ends with same vertex. Two vertices are said to be connected if there is a path between them.
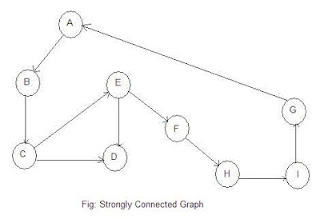
- A directed graph is strongly connected if there is a path from each vertex to every other vertex in the graph.
- A directed graph is weakly connected if at least two vertices are not connected.
- Adjacency list: An adjacency list is the representation of all edges or arcs in a graph as a list.
- Adjacency matrix: The adjacency matrix uses a vector (one-dimensional array) for the vertices and a matrix (two –dimensional array) to store the edges.
- Depth First Traversal: In the depth first traversal. We process all of the vertex’s descendants before we move to an adjacent vertex. It uses stack to store the nodes.
- Breadth – First Traversal: In the breadth – first traversal of a graph, we process all adjacent vertices of a vertex before going to the next level. The breadth – first traversal uses a queue rather than a stack. As we process each vertex, we place all of its adjacent vertices in the queue.
- Spanning trees: A spanning tree of a graph is an undirected tree consisting of only those edges necessary to connect all the nodes in the original graph.
- Network: A network is a graph that has weights or costs associated with its edges. It is also called weighted graph.
- Minimum Spanning Tree: This is a spanning tree that covers all vertices of a network such that the sum of costs of its edges is minimum. There are two algorithms which are:
- Forest: An undirected graph which contains no cycles is called a forest. A directed acyclic graph is often referred to as dag.
- Complete graph: A graph is said to be complete if there is an edge between every pair of vertices.
- Bipartite graph: A graph is said to be bipartite if the vertices can be split into sets V1 and V2. Such there are no edges between two vertices of V1 or vertices of V2.
- Uniformed search: A problem consists of four parts: the initial state, a set of operators, a goal test function, a path cost function. A path through the state space from the initial state to a goal state is a solution.
- Completeness:It is the strategy guaranteed to find a solution when there in one.
- Time complexity: It is the how long does it take to find a solution.
- Space complexity: It is the how much memory needs to perform the search.
- Optimality: Does the strategy find the highest quality solution when there are several different solutions.
Breadth first search: Expands the shallowest node in the search tree first. It is complete optimal for unit-cost operations, and has time and space complexity of O(b^d). The space complexity makes it impractical in most cases. Using BFS Strategy, the root node is expanded first, then all the nodes generated by the root node are expanded next, and their successors and so on.
Uniform cost search: Expands the least – cost leaf nod first. It is complete, and unlike breadth-first search is optimal even when operators have differing costs. It’s space and time complexity are the same as BFS.
Depth- First search: Expands the deepest node in the search tree first. It is neither complete nor optimal, and has time complexity of O(b^m) and space complexity of O(bm), where m is the maximum depth. In search trees of large of finite depth, the time complexity makes this impractical.
Depth-Limited search: Places a limit on how deep a depth-first search can go. If the limit happens to be equal to the depth of shallowest goal state, then the time and space complexity are minimized.
Iterative deepening search: Calls depth – limited search with increasing limits until a goal is found. It is completed and optimal, and has time complexity of O(b^d).
Bidirectional search: Can enormously reduce time complexity, but is not always applicable. Its memory requirements may be impractical. BDS simultaneously search both forward form the initial state and backward from the goal and stop when the two search meet in the middle.
You Might also view the following Related Posts
- Fundamental of data structures
- Definition of Stack
- Definition of Queues
- Definition of List and Linked List
- Tree







لا يوجد تعليقات
أضف تعليق